几何直观下ARCS的数学情境式学习的研究与实践

苏州大学附属尹山湖中学 俞楚寒

摘要：初中数学教学的几何直观能力培养是素质教育中的重要组成部分，几何的学习离不开情境的体验，通过ARCS动机下数学情境的创设，让学生能够在直观的情境中感悟几何，更好地探究几何的本质，发散思维。ARCS的情境式学习将几何更直观呈现，进一步培养学生的几何直观能力。

关键词：几何直观，ARCS动机模型，情境体验，学习

几何直观是初中阶段学生核心素养的主要表现之一，对于几何图形以及几何体的理解要求很高，除了需要牢记各几何图形或几何体的性质，还需要把握问题的本质，不管是对学生的学还是教师的教要求都很高。虽然要求很高，但学生与教师的重视程度还不够，只停留在表面，没有深入到问题的本质，形成模型。因此，本文就以几何直观这一核心素养能力的培养为起点，以ARCS动机模型为抓手，创新思维，研究几何直观下ARCS的数学情境式学习，以促进数学的教学品质。

一、有关数学几何直观的核心概念解读

（一）几何直观

数学的学习离不开几何，而几何的学习离不开直观的情境，因此，几何直观素养在数学学习中有着举足轻重的作用。《义务教育数学课程标准（2022年版）》在核心素养表现指出：几何直观主要是指运用图表描述和分析问题的意识与习惯。能够感知各种几何图形及其组成元素，依据图形的特征进行分类；根据语言描述画出相应的图形，分析图形的性质；建立形与数的联系，构建数学问题的直观模型；利用图形分析实际情境与数学问题，探索解决问题的思路。[1]

在新课改和素质教育背景下，要通过教师的课堂教学以及情境创设来更好地帮助学生进行几何体的理解，构建数学模型，深入数学学习。

（二）ARCS的情境式学习

情境式学习是以培养学生的直观感受为目的，它是需要借助一定的几何图形或几何体进行的学习，通过几何体的呈现，创设情境，让学生在这样的情境中学习，认识并学习几何图形或几何体，培养直观的能力。同时能够在情境学习中画出图表，分析问题，从本质上抓住问题的本质，建立直观模型，更好发展学生的几何直观能力。

ARCS模型是由美国佛罗里达州立大学的约翰·M·凯勒（John M Keller）教授予20世纪80年代提出的一个教学设计模型。所谓ARCS，是Attention（注意）、Relevance（关联）、Confidence（信心）和 Satisfaction（满意）四个英文单词的首字母的缩写。

ARCS代表了四类主要的动机策略，以ARCS为抓手围绕这四个方面来进行情景式教学，能更好激发学生在课堂学习中的动机。

二、几何直观下数学情境式学习的策略

（一）ARCS的数学情境式直观体验

1.A：Attention——观察新几何

数学重在观察，观察才能更好掌握。对于一个没有接触过的几何图形、几何体或者是小学简单学习过的几何图形、几何体都是一种新的几何，而对于这类几何的观察必不可少。

以七年级上册第5章第一节《丰富的图形世界》为例，这一节是整个一张的引入，让学生了解一些几何体，虽然生活中有很多几何体，但学生们没有深入地研究过，有的连名称也不知道，因此，这节课的观察很重要，要会认识基本的几何体，感悟几何图形是由点、线、面组成的。并且能够区分柱体与椎体的区别，通过几何体的展示来让学生直观感受到几何体的区别，能够进行归类。

在学生经历了观察的过程后，教师再加以引导，让学生能够更深入地思考与探究，不仅能提高数学上的几何直观能力，也能培养学生认识美、欣赏美、创造美的能力，实现学科间的融合。

2.R：Relevance——构建新概念

概念的构建是进行直观体验后对几何图形或几何体掌握与否最直观的映射。几何的学习不仅要靠观察，而且要能够把这些几何的组成元素列出，并通过这些元素间的不同进行概括与分类，构建一个新的概念。

以七年级下册第7章第四节《认识三角形》为例，这一节除了要通过观察认识三角形这个基本的形状外，还要厘清组成三角形的各要素，在原来学习的基础上形成新的概念，重点是三角形的中线、角平分线以及高的深入学习，不同的三角形的中线、角平分线、高之间有什么不同，在这个过程中学会分类讨论的数学思想。同时在探究的过程中分析能构成三角形的条件，将知识与知识之间联系起来，构建起新的概念。除了需要培养学生概念的构建，其实这一章对作图能力要求也很高，既要有直观的概念，又要能画出直观的图，构建双直观的知识体系。

3.C：Confidence——激发新思维

直观体验既培养学生的几何直观能力，也激发学生新的思维。教师要善于把握这一契机，引导学生探究思考，拓展学生的思维，发现不同的立足点，让教育活起来，取代灌输式的教育，逐步培养起学生学习数学的信心。

以七年级下册第7章第一节《探索直线平行的条件》为例，这一节完全可以跳出传统的教学思维，放手让学生去研究，两条直线被第三条直线所截，三线八角中满足什么样的条件能够使两直线平行，这些都是可以让学生自己去小组研究，教师需要做的就是引导，在动手作图中给出同位角、内错角、同旁内角的概念的基础上让学生自己去分析，当同位角满足什么条件时两直线刚好平行。在三线八角不断的移动变化以及小组的比较与讨论中拓展思维，得出结论：同位角相等，两直线平行。在后面的课时中更可以类比学习，激发学生新的思维，在直观的体验中有更深的认识。

4.S：Satisfaction——快乐慧学习

让学生感受到学习的价值、学习的快乐，让他们在学习中获得满足很重要。有了这样的情感基础后才能更快乐更智慧进行学习。

以八年级下册第10章第一节《分式》为例，这一节主要是认识什么样的式子是分式，同时需要知道分式有意义的条件以及分式的值。这一节内容不难，但确是中考必考的一题，学会之后，通过中考题的展示，让学生体会学习其实并没有想象中那么难，能够有学习的成就感，知道学了之后是有用的，中考可以得分，在学习中获得满足，这样能更好进行较困难的知识点的学习。

（二）“四个点”，培养学生几何直观能力

1.锁定关键点

几何学习中有许多内容，图形也是千变万化的，有的变以下位置学生就不会做了，因此教师在教学的过程中也要创设不同的情境，在情境中锁定关键点，让学生一看到图形就知道方法是什么样的。

以八年级上册第1章《全等三角形》为例，这里面其实有很多全等的图形，有时候平移旋转以下位置变了就是另一个变式，例如两个全等三角形的组合，下面举了三幅图，就是位置变化以下，条件变化以下，但本质的关键点还是不变的，因此在教育中一定要教会学生锁定关键点，关键点是把相应的角与边找出，从已知出发，熟练应用全等的判定来做题。

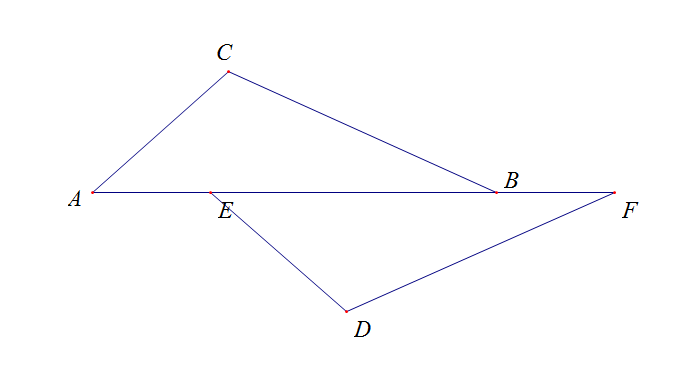
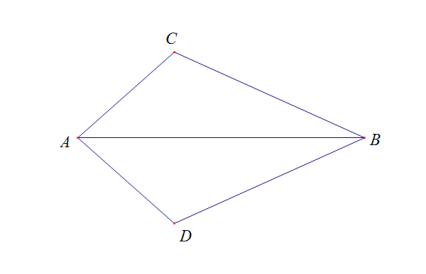
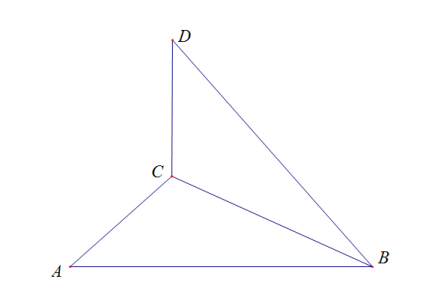
（图1） （图2） （图3）

2.关注特殊点

数学教材的排布是螺旋式的，以前学习过的知识点还会以新的形式呈现出来，几何的学习也是一样的，有的小学学习过了，初中会继续深入学习，但有些几何就很特殊，教师要引导学生在情境中讨论，总结出特殊点，并且能关注特殊点。

以八年级下册第9章《中心对称图形——平行四边形》为例，这里在探究完平行四边形的判定与性质之后开始进行矩形、菱形、正方形的学习，且在平行四边形的基础上加一定的条件变成矩形、菱形、正方形，它们也叫做“特殊的平行四边形”，拥有平行四边形所有的性质，并且还有它们特殊的性质。在这些几何图形的学习中，教师要给出具体的情境，让学生在情境中探究，并且关注特殊的点，比如平行四边形加一个特殊的条件——对角线相等，就可以变成矩形了。

3.把握迁移点

学习中的迁移是指一种学习对另一种学习的影响，或用所得到的经验完成其他学习，而常见的数学迁移是知识与技能的迁移。对于几何的学习来说，迁移能力更是重要。在核心素养理念下，教师要切实提高学生的几何直观能力，利用情境通过启发、联想、提示等方法灵活迁移，帮助学生把握迁移点，在数学学习中学会迁移应用，改善学习效果。[2]

以七年级上册第6章《平面图形的认识（一）》为例，这一章先是学习线段的概念，继而进一步比较线段的大小，学习线段的和差倍分。有了线段学习的基础，在学习角的时候就是知识的迁移，在实际教学中教师也会发现教材的编排与线段那一节的编排几乎一样，因此在学习角的时候其实是可以放手交给学生解决的，将已有的学习线段的经验迁移到角的和差倍分的学习中，更好地培养学生的迁移能力，能够在众多的知识中把握迁移点。

4.衔接练习点

对于学生几何能力的培养只在课堂是不够的，还要注重课后的练习，教师可以上课的题目为例，针对性地设计课后的作业，一类是课堂讲过的一样的题目的再练，另一类是需要自己思考的变式，用这两类来巩固发展学生的几何直观能力。

以九年级上册第2章第6节《正多边形与圆》为例，上课可以通过三角形与圆的关系入手，继而学习四边形与圆的关系，课后则可以先从这几方面布置作业，让学生们巩固课上所学的知识点，再可以拓展以下五边形、六边形与圆的关系，用同样的方法研究，既是对知识点的巩固也是一次很好的培养几何独立解题的能力。

初中数学教学的几何直观能力培养是素质教育中的重要组成部分，对学生及教师都提出了较高的要求。几何直观下数学的情境式学习能够更好帮助学生观察几何、掌握几何的性质，发展学生的几何直观能力。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社,2022:4

[2]陈怡.试论核心素养理念下数学迁移能力的培养[J].成才之路,2020(33):96-97.

[3]吴临英.初中数学几何直观能力培养探析[J].文理导航(中旬),2022(12):73-75.